Matrix Calculus¶
Kindergarten definitions¶
Gradient¶
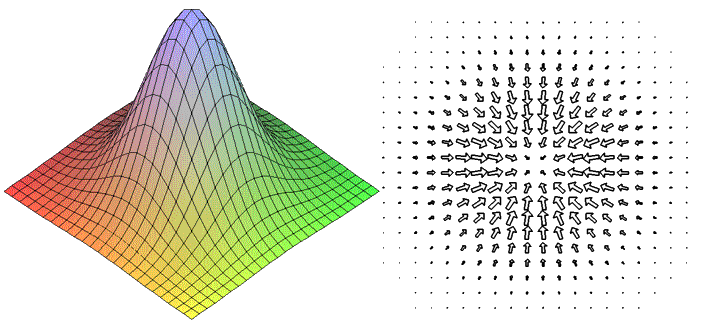
Let $f(x): \mathbb{R}^n \to \mathbb{R}$, then vector, which contains all first order partial derivatives: $$\nabla f(x) = \dfrac{df}{dx} = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{pmatrix}$$ named gradient of $f(x)$. This vector indicates the direction of steepest ascent. Thus, vector $- \nabla f(x)$ means the direction of the steepest descent of the function in the point. Moreover, the gradient vector is always orthogonal to the contour line in the point.
$$\nabla f(x)^T = \dfrac{df}{dx^T} = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n} \right)$$
Hessian¶
Let $f(x): \mathbb{R}^n \to \mathbb{R}$, then matrix, containing all the second order partial derivatives: $$f''(x) = \dfrac{d(\nabla f)}{dx^T} = \dfrac{d\left(\nabla f^T\right)}{dx} = \begin{pmatrix} \frac{\partial^2 f}{\partial x_1 \partial x_1} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \dots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2 \partial x_2} & \dots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \dots & \frac{\partial^2 f}{\partial x_n \partial x_n} \end{pmatrix}$$
But actually, Hessian could be a tensor in such a way: $\left(f(x): \mathbb{R}^n \to \mathbb{R}^m \right)$ is just 3d tensor, every slice is just hessian of corresponding scalar function $\left( H\left(f_1(x)\right), H\left(f_2(x)\right), \ldots, H\left(f_m(x)\right)\right)$
Jacobian¶
The extension of the gradient of multidimensional $f(x): \mathbb{R}^n \to \mathbb{R}^m$: $$f'(x) = \dfrac{df}{dx^T} = \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \dots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \dots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \dots & \frac{\partial f_m}{\partial x_n} \end{pmatrix}$$
Matrix and vector derivatives¶
Table¶
$$f(x) : X \to Y; \;\;\;\;\;\;\;\; \frac{\partial f(x)}{\partial x} \in G$$
| X | Y | G | Name |
|---|---|---|---|
| $\mathbb{R}$ | $\mathbb{R}$ | $\mathbb{R}$ | $f'(x)$ (derivative) |
| $\mathbb{R}^n$ | $\mathbb{R}$ | $\mathbb{R^n}$ | $\dfrac{\partial f}{\partial x_i}$ (gradient) |
| $\mathbb{R}^n$ | $\mathbb{R}^m$ | $\mathbb{R}^{n \times m}$ | $\dfrac{\partial f_i}{\partial x_j}$ (jacobian) |
| $\mathbb{R}^{m \times n}$ | $\mathbb{R}$ | $\mathbb{R}^{m \times n}$ | $\dfrac{\partial f}{\partial x_{ij}}$ |
The notation of differentials could be useful here¶
- $dA = 0$
- $d(\alpha X) = \alpha (dX)$
- $d(AXB) = A(dX )B$
- $d(X+Y) = dX + dY$
- $d(X^\top) = (dX)^\top$
- $d(XY) = (dX)Y + X(dY)$
- $d\langle X, Y\rangle = \langle dX, Y\rangle+ \langle X, dY\rangle$
- $d\left( \dfrac{X}{\phi}\right) = \dfrac{\phi dX - (d\phi) X}{\phi^2}$
- $d\left( \det X \right) = \det X \langle X^{-\top}, dX \rangle $
- $d \text{tr } X = I$
- $df(g(x)) = \dfrac{df}{dg} \cdot dg(x)$
I order approximation $$ df(x) = \langle \nabla f(x), dx\rangle $$
II order approximation
$$ d^2f(x) = \langle \nabla^2 f(x) dx_1, dx_2\rangle = \langle H_f(x) dx_1, dx_2\rangle $$
Solution:
- $f(x) = \sum\limits_{i=1}^n c_i x_i$
- $\dfrac{\partial f(x)}{\partial x_k} = c_k \rightarrow \nabla f(x) = c$
Example 1.2¶
Calculate $\nabla f(x)$, if $f(x) = \dfrac{1}{2}x^TAx + b^Tx + c$
Solution:
- $f(x) = \sum\limits_{i=1}^n\left[ \dfrac{1}{2}x_i \left(\sum\limits_{j=1}^n a_{ij}x_j \right) + b_ix_i + c_i\right] = \dfrac{1}{2} \sum\limits_{i,j=1}^n\left[ x_i a_{ij}x_j \right] + \sum\limits_{i=1}^n b_ix_i + c_i$
- $\dfrac{\partial f(x)}{\partial x_i} = \dfrac{1}{2}\sum\limits_{i,j=1}^n \left(a_{ij} + a_{ji}\right)x_i + b_i \rightarrow \nabla f(x) = \dfrac{1}{2} \left( A + A^T \right)x + b$
Example 1.3¶
Calculate $\nabla f(x), f''(x)$, if $f(x) = -e^{-x^Tx}$
Решение:
- $f(x) = - e ^{-\sum\limits_i x_i^2}$
- Let's calculate one component of gradient vector: $$\dfrac{\partial f(x)}{\partial x_k} = - e ^{-\sum\limits_i x_i^2} \cdot \left( \dfrac{\partial (-\sum\limits_i x_i^2)}{\partial x_k} \right) = e ^{-\sum\limits_i x_i^2} \cdot 2x_k$$ Thus, we can state, that $\nabla f(x) = 2 e^{-x^Tx} \cdot x$
Absolutely the same logic could be $$g_k = \dfrac{\partial f(x)}{\partial x_k} \rightarrow H_{k,p} = \dfrac{\partial g_k}{\partial x_p}$$ $$H_{k,p} = - \left( e ^{-\sum\limits_i x_i^2} \cdot 2x_p\right) 2x_k + 2 e ^{-\sum\limits_i x_i^2} \dfrac{\partial x_k}{\partial x_p} = 2 e ^{-\sum\limits_i x_i^2} \cdot \left( \dfrac{\partial x_k}{\partial x_p} - 2x_px_k\right)$$
Finally, $f''(x) = H_{f(x)} = 2e^{-x^Tx} \left( E - 2 xx^T\right)$
Example 2.1¶
Calculate $\nabla f(x)$, if $f(x) = \dfrac{1}{2} \|Ax - b\|^2_2$
Solution:
$$ f(x) = \dfrac{1}{2} \langle Ax-b, Ax-b\rangle $$
$$ d f(x) = \dfrac{1}{2} 2 \langle Ax-b, Adx\rangle $$
$$ d f(x) = \langle A^\top(Ax-b), dx\rangle \;\;\;\; \to \nabla f(x) = A^\top (Ax-b) $$
Example 2.2¶
Calculate $\nabla f(x)$, if $f(x) = \ln \langle Ax, x \rangle$
Solution:
$$ df(x) = \dfrac{d\langle Ax, x \rangle}{\langle Ax, x \rangle} = \dfrac{Ad\langle x, x \rangle}{\langle Ax, x \rangle} = \dfrac{2A \langle x, dx \rangle}{\langle Ax, x \rangle} = \dfrac{2\langle Ax, dx \rangle}{\langle Ax, x \rangle} $$
Example 2.3¶
Calculate $\nabla f(X)$, if $f(X) = \text{tr } AX$
Solution:
$$ f(X) = \langle A^\top, X\rangle $$
$$ d f(X) = d \langle A^\top, X\rangle = \langle A^\top, dX\rangle $$
$$ \nabla f(X) = A^\top $$
Example 2.4¶
Calculate $\nabla f(X)$, if $f(X) = \langle S, X\rangle - \log \det X$
Solution:
$$ df(X) = \langle S, dX \rangle - \dfrac{d(\det X)}{\det X} $$
$$ df(X) = \langle S, dX \rangle - \dfrac{\det X \langle X^{-\top}, dX\rangle}{\det X} $$
Suppose, that $\det X \neq 0$
$$ df(X) = \langle S, dX \rangle - \langle X^{-\top}, dX\rangle = \langle S - X^{-\top} , dX\rangle $$